The Fibonacci Rabbit sequence

Other names for the Rabbit Sequence are the Golden Sequence because, as we shall see, it is closely related to the golden section numbers Phi (=1.6180339..) and phi=(0.6180339..).

Fibonacci Numbers and the Rabbit sequence

This page is all about a remarkable sequence of 0s and 1s which is intimately related to the Fibonacci numbers and to Phi:

1 0 1 1 0 1 0 1 1 0 1 1 0 1 0 1 1 0 1 0 1 1 0 1 1 0 1 0 1 1 0 1 ...

First we re-examine Fibonacci's original Rabbit problem and see how it can generate an infinite sequence of two symbols and in a later section we see how the same sequence is very simply related to Phi also.

Lining up the Rabbits

If we return to Fibonacci's original problem - about the rabbits then we start with a single New pair of rabbits in the field. Call this pair N for "new".

  Month 0:
        N

Next month, the pair become Mature, denoted by "M".

  Month 0:  1:
        N   M

The following month, the M becomes "MN" since they have produced a new pair (and the original pair also survives).

  Month 0:  1:  2:
        N   M   M
                N

The M of month 2 become MN again and the N of month 2 has become M, so month 3 is: "MNM"

  Month 0:   1:   2:   3:
        N -  M -  M -  M
                \   \  N
                  N -  M

The next month it is "MNMMN".

The general rule is

replacing every M in one month by MN in the next and similarly replace every N by M.

Hence MNM goes to MN M MN .

We have now got a collection of sequences of M's and N's which begins:

   0: N            =N
   
   1: M            =M
   
   2: M      N     =MN
   
   3: M   N  M     =MNM
   
   4: M N M  M N   =MNMMN
   
   5: MNM MN MNM   =MNMMNMNM
      ...           ...

Compare this with the picture we had of the Rabbit Family Tree where sometimes M is replaced by NM and sometimes by MN.

We often use 1s and 0s for this sequence, so here we have replaced M by 1 and N by 0:

Another way to generate The Rabbit sequence

We can make the rabbit sequence for month x by taking the sequence from month x-1 and writing it out again, following it by a copy of the sequence of month x-2.

So, starting from N and M the next is M (last month) followed by N (the previous month) giving MN.

The next will be MN followed by M = MNM

and the one after that is MNM followed by MN = MNMMN.

From this definition we can see that
each monthly sequence is the start of the following month's sequence.

This means that (after the first sequence which begins with N), there is really just one infinitely long sequence, which we call the rabbit sequence or the golden sequence or the golden string.

The first 2000 bits of the Rabbit Sequence

1011010110 1101011010 1101101011 0110101101 0110110101 50

1010110110 1011011010 1101011011 0101101101 0110101101 100

1010110101 1011010110 1101011010 1101101011 0101101101

0110110101 1010110110 1011011010 1101011011 0101101011 200

0110101101 1010110101 1011010110 1101011010 1101101011

0101101101 0110110101 1010110110 1011010110 1101011011 300

0101101011 0110101101 1010110101 1011010110 1011011010

1101101011 0101101101 0110101101 1010110110 1011010110 400

1101011011 0101101011 0110101101 0110110101 1011010110

1011011010 1101101011 0101101101 0110101101 1010110110 500

1011010110 1101011010 1101101011 0110101101 0110110101
1011010110 1011011010 1101011011 0101101101 0110101101
1010110110 1011010110 1101011010 1101101011 0110101101
0110110101 1010110110 1011011010 1101011011 0101101101
0110101101 1010110101 1011010110 1101011010 1101101011
0101101101 0110110101 1010110110 1011011010 1101011011
0101101011 0110101101 1010110101 1011010110 1101011010
1101101011 0101101101 0110110101 1010110110 1011010110
1101011011 0101101011 0110101101 1010110101 1011010110
1011011010 1101101011 0101101101 0110101101 1010110110

1011010110 1101011011 0101101011 0110101101 0110110101
1011010110 1011011010 1101101011 0101101101 0110101101
1010110110 1011010110 1101011010 1101101011 0110101101
0110110101 1011010110 1011011010 1101011011 0101101101
0110101101 1010110110 1011010110 1101011010 1101101011
0110101101 0110110101 1010110110 1011011010 1101011011
0101101101 0110101101 1010110101 1011010110 1101011010
1101101011 0101101101 0110110101 1010110110 1011011010
1101011011 0101101011 0110101101 1010110101 1011010110
1101011010 1101101011 0101101101 0110110101 1010110110

1011010110 1101011011 0101101011 0110101101 1010110101
1011010110 1011011010 1101101011 0101101101 0110110101
1010110110 1011010110 1101011011 0101101011 0110101101
0110110101 1011010110 1011011010 1101101011 0101101101
0110101101 1010110110 1011010110 1101011010 1101101011
0110101101 0110110101 1011010110 1011011010 1101011011
0101101101 0110101101 1010110110 1011010110 1101011010
1101101011 0110101101 0110110101 1010110110 1011011010
1101011011 0101101101 0110101101 1010110101 1011010110
1101011010 1101101011 0101101101 0110110101 1010110110 2000

Fractals

There is a lot of interest currently in Fractals. A Fractal is a shape or sequence or system that is infinite and contains a copy of itself within itself. Such pictures or series are called self-replicating or self-generating.

Our golden string contains copies of itself inside it. To see this we first show another way in which we can write down the golden string.

Another way to make the Fibonacci Rabbit sequence

Above, we started with M and then replaced M by MN. From then on, we repeatedly replace M by MN and each N by M which was the process whereby we made the Fibonacci rabbit sequence at the top of this page.

Combining this with the fact that each time we replace all the letters and get a new string, the fact that the old string is the start of the new string, then we have the following simple method of generating the golden sequence (we use 1 for M and 0 for N so that it gives the list of bits above):

Start by writing 10 (which stands for MN above) and point to the second symbol, the 0, with your left hand.

Keep your right hand ready to add some more symbols at the end of the same sequence.

Use the symbol pointed at by your left hand to determine how to extend the sequence at the right hand end:

If the symbol you are pointing at with your left hand is a 1, then, with your right hand, write 10 (at the end of the string);
If your left hand is pointing at a 0 then write 1 with your right hand.

In both cases, then move your left hand to point to the next symbol along.

Repeat the step 2 for as long as you like. Here is how the process starts, where the ^ indicates the symbol pointed at by our left hand:

   10   
    ^     We are pointing at 0, so write a 1 at the end, 
   101
    ^     and move the left hand on one place on (to point to the new symbol in fact):
   101 
     ^    We are pointing at a 1, so write 10 at the end 
   10110
     ^    and move the left hand on one place:
   10110 
      ^   We are pointing at a 1 so write 10 at the end
   1011010
      ^   and move the left hand on one place:
   1011010  ...
       ^

Here is the algorithm

 
   Start with sequence 10, pointing at the 0.
   (Step 1) if pointing at 0 
               then write 1 on to the end of the sequence;
         OR if pointing at 1 
               then write 10 at the end;
   (Step 2) Now point at the next symbol along
   (Step 3) Start again at step 1.

and below it is shown as an animated gif image:

Since we are writing more symbols than we are "reading", the sequence never ends.

Fibonacci and the Mandelbrot Set

The Mandelbrot set shown here has been written about often in maths books, appears in magazines and posters, greeting cards and wrapping paper and in lots of places on the Net.

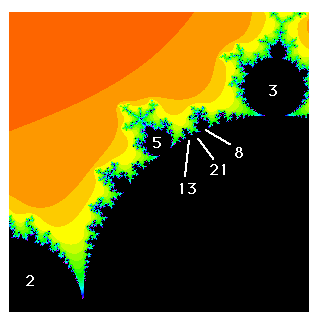
A detail from the Mandelbrot set picture is shown here. It is also a link to a page on how the Fibonacci numbers occur in the Mandelbrot Set (at Boston University Mathematics Department).