The Golden Section in Art, Architecture
and Music
This section introduces
you to some of the amazing applications and occurrences of the Fibonacci
series and the Golden Ratio in architecture, art and in music.
The Golden section in architecture
Even from the time of the
Greeks, a rectangle whose sides are in the proportion of two neighbouring
Fibonacci numbers has been a seen as a pleasing shape. Such rectangles
are approximations of the golden rectangle whose sides are in the ratio
of 1:Phi = 1:1.618033 or, equivalently, phi:1=0.618033:1. It appears in
many of the proportions of the ancient Greek temple, the Parthenon, in
Athens, Greece. (There is a replica of the original building (accurate
to one-eigth of an inch!) at Nashville which calls itself "The Athens of
South USA".)
The Acropolis, in the centre
of Athens, Greece, is an outcrop of rock that dominates this ancient city.
It's most famous monument, now largely ruined, is the Parthenon, a temple
to the goddess "Athena" built around 430/440BC.
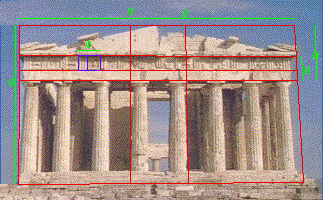
The plan shows that the
temple was built on a square-root-of-5 rectangle, that is, it is 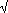 5
times as long as it is wide. It's front elevation is built on a Golden
Ractangle, that is, it is Phi times as wide as it is tall.
5
times as long as it is wide. It's front elevation is built on a Golden
Ractangle, that is, it is Phi times as wide as it is tall.
Le Corbusier often used golden
rectangles in the shapes of the buildings he designed. One of these is
the United Nations building in New York which is L-shaped. The upright
part of the L has sides in the golden ratio, and there are distinctive
marks on this taller part which divide the height by the golden ratio.
The United Nations Headquarters On-line Tour has an aerial view of the
building (with thanks to Ralph Bechtolt for alerting me to this link).
The Golden Section and Art
Lucas Pacioli (1445-1517)
in his Divina proportione (On Divine Proportion) wrote about the
golden section also called the golden mean or the divine
proportion:
A M B
| 1-x | x |
The line AB is divided at
point M so that the ratio of the two parts, the smaller to the larger (AM
and MB), is the same as the ratio of the larger part (MB) to the whole
AB.
If AB is of length 1 unit,
and we let MB have length x, then the definition (in bold) above becomes
the ratio of 1-x to x
is the same as the ratio of x to 1 or, in symbols:
1 - x = x which simplifies to 1-x = x2
x 1
This gives two values for x,
(-1-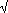 5)/2 and (
5)/2 and (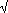 5-1)/2.
5-1)/2.
The first is negative, so
does not apply here. The second is just phi (which has the same value as
1/Phi and as Phi-1).
Pacoli's work influenced Leonardo
da Vinci (1452-1519) and Albrecht Durer (1451-1578) and is seen in some
of the work of Georges Seurat, (for example La Parade) and Paul Signac
and Mondrian, for instance.
 Many books on oil painting and
water colour in your local library will point out that it is better to
position objects not in the centre of the picture but to one side or "about
one-third" of the way across, and to use lines which divide the picture
into thirds. This seems to make the picture design more pleasing to the
eye and relies again on the idea of the golden section being "ideal".
Many books on oil painting and
water colour in your local library will point out that it is better to
position objects not in the centre of the picture but to one side or "about
one-third" of the way across, and to use lines which divide the picture
into thirds. This seems to make the picture design more pleasing to the
eye and relies again on the idea of the golden section being "ideal".
Leonardo's Art
The Uffizi Gallery's Web
site in Florence, Italy, has a virtual room of some of Leonardo da Vinci's
paintings. Here are two for you to analyse for yourself. [The pictures
are links to the Uffizi Gallery site and the pictures are copyrighted by
the Gallery.]
-

-
-
The Annunciation
-
is a picture that looks like
it is in a frame of 1:sqrt(5) shape (a root-5 rectangle). Print it and
measure it - is it a root-5 rectangle? Divide it into a square on the left
and another on the right. (If it is a root-5 rectangle, these lines mark
out two golden-section rectangles as the parts remaining after a square
has been removed). Also mark in the lines across the picture which are
0.618 of the way up and 0.618 of the way down it. Also mark in the vertical
lines which are 0.618 of the way along from both ends. You will see that
these lines mark out significant parts of the picture or go through important
objects. You can then try marking lines that divide these parts into their
golden sections too.
-
-

-
-
Madonna with Child and Saints
-
is in a square frame. Print
it out and mark on it the golden section lines (0.618 of the way down and
up the frame and 0.618 of the way across from the left and from the right)
and see if these lines mark out significant parts of the picture. Do other
sub-divisions look like further golden sections?
Fibonacci and Poetry
Martin Gardner, in the chapter
"Fibonacci and Lucas Numbers" in "Mathematical Circus" (Penguin books,
1979) mentions Prof George Eckel Duckworth's book Structural patterns
and proportions in Vergil's Aeneid : a study in mathematical composition
(University of Michigan Press, 1962). Duckworth argues that Vergil
consciously used Fibonacci numbers to structure his poetry and so did other
Roman poets of the time.
Fibonacci and Music
There is a fascinating section
in T H Garland's book [see below] on the 5-tone scale (the black notes
on the piano), the 8-tone scale (the white notes on the piano) and the
13-notes scale (a complete octave in semitones, with the two notes an octave
apart included).
Various composers have used
the Fibonacci numbers when composing music - more details in Garland's
book.
Golden sections in Violin construction
The section on "The Violin"
in The New Oxford Companion to Music, Volume 2, shows how Stradivari was
aware of the golden section and used it to place the f-holes in his famous
violins.
Baginsky's method of contructing
violins is also based on golden sections.
Did Mozart use the Golden mean?
This is the title of an article
in the American Scientist of March/April 1996 by Mike Kay. He reports on
the analysis of many of Mozart's sonatas and finds they divide into two
parts exactly at the golden section point in almost all cases. Was this
a conscious choice (his sister said he was always playing with numbers
and was fascinated by mathematics) or did he do this intuitively?
Beethoven's FIfth
In an interesting little
article in Mathematics Teaching volume 84 in 1978, Derek Haylock
writes about The Golden Section in Beethoven's Fifth on pages 56-57.
He finds that the famous
opening "motto" appears not only in the first and last bars (bar 601 before
the Coda) but also exactly at the golden mean point 0.618 of the way through
the symphony (bar 372) and also at the start of the recapitulation which
is phi or 0.382 of the way through the piece! He poses the question:
Was this by design
or accident?
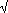 5
times as long as it is wide. It's front elevation is built on a Golden
Ractangle, that is, it is Phi times as wide as it is tall.
5
times as long as it is wide. It's front elevation is built on a Golden
Ractangle, that is, it is Phi times as wide as it is tall.




